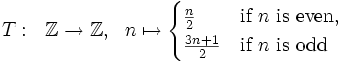
The derived subgroup G' of a group G is defined as the group generated by all commutators [a,b] := a^-1b^-1ab, where a,b ∈ G. In general, not all elements of the derived subgroup of a group are actually commutators themselves. Find a group G of smallest possible order such that the set of all commutators of elements of G does not form a group!
Commutators can be computed by the operation Comm, and the derived subgroup can be computed by the operation DerivedSubgroup. The function Cartesian and the operations Set and AsList can be helpful in this context as well. If you are lazy but patient, you may simply use CommutatorLength. Otherwise, this exercise requires writing a couple of lines of GAP code. The wanted group has order greater than 50, but less than 100.
For a solution, see Section 2.1.
Is there a finite group which has an automorphism which is not inner, but which nevertheless fixes all conjugacy classes setwise? -- If so, then find an example of least possible order!
This exercise is slightly more difficult than that given in Section 1.1. Useful functions and operations are AllGroups, AutomorphismGroup, IsInnerAutomorphism, IsConjugate, Image and AsList. It is a good exercise to try to find a way to write down the group and the automorphism in a nice and human-readable form. One possible way to achieve this is to determine a "nice" permutation representation of the group, and to choose an automorphism with the desired property which fixes all but one of the generators.
For a solution, see Section 2.2.
Write a GAP function which draws the Ulam spiral and saves the picture in a file!
The arguments of the function should be the size (width / height) of the picture to be drawn and the name of the output file.
This is more or less just an easy programming exercise, which does not require particular mathematical knowledge. Use the function NullMat to create a zero matrix over the field with two elements, and use this matrix as a grid to draw the spiral. The RCWA package [Koh07b] provides a function SaveAsBitmapPicture, which can be used to produce a picture file from the matrix.
For a solution, see Section 2.3.
The automorphisms of a finite projective plane are determined by the permutations of the set of points which move lines to lines. Thus, labelling the points with integers 1, 2, dots, n, the automorphism group can be described as a subgroup of the symmetric group S_n.
The smallest projective plane has 7 points and 7 lines. Any point is incident with 3 lines, and any line is incident with 3 points. We label the points with integers 1, 2, dots, 7. Then the lines are given by the sets g_1 := {1,2,3}, g_2 := {1,4,7}, g_3 := {1,5,6}, g_4 := {2,4,6}, g_5 := {2,5,7}, g_6 := {3,4,5} and g_7 := {3,6,7} of points which are incident with them.
Compute the automorphism group of the smallest projective plane!
A useful function in this context is SubgroupProperty. The actual determination of the group can be done in one statement. Can you figure out the isomorphism type of the group by theoretical means?
For a solution, see Section 2.4.
What happens when you enter the command Centre(AlternatingGroup(100)); in GAP? Are you satisfied with the performance, given that the centre of a nonabelian simple group is always trivial and that GAP knows that the alternating group of degree 100 is simple?
Probably not. -- Thus improve the performance radically by implementing a method for Centre for simple groups, which returns either the group itself or the trivial subgroup, depending on whether the group is abelian or not!
Methods are installed with InstallMethod. The exercise is easy -- basically all you need to do is to look up in the documentation how this function is used. If your solution is correct, then Centre(AlternatingGroup(100)); returns the trivial subgroup immediately, and Centre(G) still computes the centre of a non-simple group G using methods implemented in the GAP Library.
For a solution, see Section 2.5.
Given a positive integer n, let rad(n) denote the product of distinct prime divisors of n. The abc conjecture states that for any ϵ > 0 there is a constant K_ϵ such that for any triple (a,b,c) of coprime positive integers satisfying the equation a + b = c we have c < K_ϵ rad(abc)^1 + ϵ.
A triple (a,b,c) of coprime integers satisfying a + b = c is called an abc triple if rad(abc) is less than c. An abc triple (a,b,c) is called a good abc triple if it satisfies even ln(c)/ln( rad(abc)) > 1.4. The left-hand side of the inequality is sometimes called the ratio of the abc triple.
It can be shown easily that there are infinitely many abc triples, but if the abc conjecture holds, there are only finitely many good abc triples.
Write a GAP function which finds all good abc triples (a,b,c) with given radical rad(abc) and with c less than a given bound!
Can you find a new triple, which is not yet on Abderrahmane Nitaj's list of known good abc triples?
You can start by determining all positive integers less than the given bound all of whose prime factors divide the given radical. This can be done much more efficiently than by the Sieve of Eratosthenes, or even by looping over all integers in the range and factoring -- it is easy and very elementary to find out how. Then you can loop over all pairs of these integers, test whether they are coprime and compute the ratio if they are. To compute the ratio, you need the operation Float which converts integers and rationals to floating point numbers, and the function LOG_FLOAT which computes the natural logarithm of a floating point number.
For a solution, see Section 2.6.
Determine all undirected graphs with 6 vertices up to isomorphism! -- How many isomorphism types of such graphs are there?
The graphs should be represented as sets of edges, where the edges should be written as sets of two vertices, each.
Example: In this representation, the graphs [[1,2],[1,6],[2,3],[3,4],[4,5],[5,6]] and [[1,5],[1,6],[2,4],[2,6],[3,4],[3,5]] are both isomorphic to the regular hexagon.
Write a function GraphAutomorphismGroup(Gamma,n) which computes the automorphism group of the graph Gamma with n vertices. -- The automorphisms are precisely the permutations of the set of vertices which move edges to edges.
Note that the cardinality n of the set of vertices needs to be specified, as there may be isolated vertices.
Find out which of the (up to conjugation in S_6) 16 transitive permutation groups of degree 6 occur as automorphism groups of graphs with 6 vertices! -- How do the corresponding graphs look like?
You can obtain the set of all graphs with n vertices in the suggested notation by Combinations(Combinations([1..n],2));. Then you need to find a suitable group action on this set such that two graphs are isomorphic if and only if they lie in the same orbit. Useful operations are Orbits and Representative.
In principle you can implement a fancy algorithm here, but for our purposes a very basic one is perfectly sufficient. First find out how to check whether a given permutation of the vertices induces a graph automorphism. Then you can use SubgroupProperty to determine the group formed by all such permutations.
Given Part a) and b), this is more or less straightforward. Useful functions / operations are AllTransitiveGroups, NrMovedPoints and TransitiveIdentification.
For a solution, see Section 2.7.
Answer the following questions using GAP:
In how many ways can 1 ∈ S_4 be written as a product of exactly 100 transpositions?
In how many ways can a horse cross the chess board from the upper left to the lower right corner with exactly 100 moves?
Construct a matrix x ∈ Z^n × n with ones at suitable positions and zeros everywhere else and compute powers. For Part a), choose n := 24, and for Part b), choose n := 8^2 = 64. Useful functions are e.g. NullMat, SymmetricGroup, Combinations, Cartesian and Position.
For a solution, see Section 2.8.
By Fermat's little theorem, for any prime number p we have p|2^p-1-1. A prime number p is called a Wieferich prime if it satisfies even p^2|2^p-1-1.
Write a GAP function which checks whether a given positive integer is a Wieferich prime, and try to find as many Wieferich primes as you can!
Writing the GAP function is easy. Use PowerModInt instead of first computing 2^p-1 and then reducing modulo p^2. Two Wieferich primes can be found easily, but finding a third one is at least hard.
For a solution, see Section 2.9.
Write a GAP function which, given a filename, returns a word distribution statistics. The function should return a list with entries of the form [ "word", 237 ] for any word in the file, indicating the word and the number of times it occurs. A "word" in our sense is a sequence of letters with no non-letter characters in between, i.e. it does not need to be a dictionary word. Can you put your function into one line with no more than 80 characters?
You will probably need the operation Collected. Further, the functions StringFile and WordsString from the GAPDoc package [LN06] will be useful.
For a solution, see Section 2.10.
A group G is called metabelian if it has an abelian normal subgroup N such that the quotient G/N is abelian as well. Further, a group is called a p-group if its order is a power of a prime.
Find a non-metabelian p-group of least possible order!
First determine conceivable orders of non-metabelian groups by means of theory. Then just run a brute-force search over the groups of the smallest few of these orders in the Small Groups Library [BEO07]. Useful functions / operations are AllGroups, DerivedSubgroup and IsAbelian. For a solution, see Section 2.11.
Let σ denote the sum-of-divisors function. Given a positive integer n, let H(n) := ∑_k=1^n 1/k be the nth harmonic number, and put B(n) := H(n) + ln(H(n)) ⋅ e^H(n).
Examples are σ(24) = 60 and B(24) ≈ 61.7575, as well as σ(60) = 168 and B(60) ≈ 170.977.
Can you find an integer n > 1 such that σ(n) is larger than B(n)?
In GAP, σ(n) can be computed by Sigma(n). Use the operation Float to convert integers and rationals to floating point numbers, and use the functions LOG_FLOAT and EXP_FLOAT to compute logarithms and to evaluate the exponential function, respectively. Be prepared that finding an integer n > 1 such that σ(n) is larger than B(n) is not easy.
For a solution, see Section 2.12.
Pell's equation is any Diophantine equation of the form x^2 - ny^2 = 1, where n is a nonsquare integer.
Write a GAP function which takes an argument n and returns the smallest solution of the equation x^2 - ny^2 = 1 in positive integers!
This solution is called the fundamental solution. Your function should return for example the answer for n = 421 very quickly.
Useful functions in this context are ContinuedFractionExpansionOfRoot and ContinuedFractionApproximationOfRoot.
For a solution, see Section 2.13.
Obviously, the automorphism groups of both the trivial group and the cyclic group of order 2 are trivial, and have therefore odd order. Find the smallest group of order greater than 2 whose automorphism group has odd order!
First try to exclude the groups of even order by means of theory. Then run a brute-force search over the Small Groups Library [BEO07]. Useful functions / operations in this context are AllGroups and AutomorphismGroup.
For a solution, see Section 2.14.
Find an odd positive integer n such that n+2^k is composite for any positive integer k! -- Can you find the least possible such n?
First perform a brute-force search to find candidates. Then try to verify whether these candidates indeed have the desired property. A useful function in this context is OrderMod. In addition, it may be worth to have a look at the ResClasses package [Koh07c], and there in particular at the function ResidueClass. Finding a good candidate for the least possible number with the given property is reasonably easy, but the verification that it is indeed the smallest one is computationally difficult.
For a solution, see Section 2.15.
Write a GAP function which computes all rational points on the unit sphere x^2+y^2+z^2=1 which correspond to solutions of the diophantine equation a^2+b^2+c^2=d^2 with a, b and c not exceeding a given bound. Further, your function should draw a picture showing the projection of one octant of the sphere to the x-y-plane, where the rational points are marked by black pixels.
Just write a nested loop to determine the solutions. Note that the variables can be permuted, thus you can assume a ≥ b ≥ c and generate the solutions not satisfying this inequality by permuting a, b and c. This saves almost 5/6 of the time. Maybe a useful function in this context is Arrangements. Create an empty grid over GF(2) by the function NullMat, invert it (i.e. replace zeros by ones) and mark the solutions by zeros there. Finally, the RCWA package [Koh07b] provides a function SaveAsBitmapPicture, which can be used to write the picture to a file.
For a solution, see Section 2.16.
Given a positive integer n, the Aliquot sequence n = a_1, a_2, a_3, a_4, dots starting at n is defined by a_i+1 = σ(a_i) - a_i, where σ denotes the sum-of-divisors function. We say that the Aliquot sequence starting at n stops if there is an index i such that a_i = 1, and we say that it runs into a cycle if there are distinct indices i and j such that a_i = a_j.
Find out whether all Aliquot sequences starting at integers n < 100 either stop or run into cycles! -- Can you do the same for all Aliquot sequences starting at integers n < 200 or n < 300? Do you see algorithmic problems, and of which kind are they?
In GAP, σ(n) can be computed by Sigma(n). Computing σ(n) requires factoring n. For this, the GAP Library method for the operation Sigma calls the GAP Library function FactorsInt directly. This works for small n, but for larger n, FactorsInt will often give up and raise an error message which suggests to use the FactInt package [Koh07a]. If you have loaded FactInt, you may find this strange. However, this has nothing to do with FactInt, as this package does not get a chance to help with factoring. You can make Sigma benefit from FactInt if you fetch the method for Sigma from lib/numtheor.gi, put it into a separate file, replace FactorsInt by Factors, increase the method rank to something like SUM_FLAGS and read this file into GAP. Alternatively you can make the change directly in the GAP Library. Then you do not need to increase the method rank, but (as after every Library change) you need to rebuild the completion files. For this, start GAP with option -N and enter CreateCompletionFiles();.
For a solution, see Section 2.17.
Hofstadter's Q sequence is defined by Q_1 = Q_2 = 1 and Q_n = Q_n-Q_n-1} + Q_n-Q_n-2} for n > 2.
Write a GAP function which takes an integer argument l and computes the first l terms of the Q sequence.
Write a GAP function which plots the graph of the Q sequence.
The Q sequence is defined recursively. Ask yourself the question why a recursive implementation is not a particularly good idea in this case, anyway.
Use the function NullMat to create a zero matrix over the field with two elements, turn the zeros into ones if you prefer a black graph on a white background to a white graph on a black background, and use this matrix as a grid to draw the graph. The RCWA package [Koh07b] provides a function SaveAsBitmapPicture, which can be used to produce a picture file from the matrix.
For a solution, see Section 2.18.
Have a look at the following function, which takes as arguments three nonnegative integers and which returns a positive integer:
f := function ( i, j, k )
if i = 0 then
if j = 0
then if k = 0 then return 2; else return 2^f(i,j,k-1); fi;
else return f(i,j-1,f(i,j-1,k)); fi;
else
return f(i-1,f(i-1,j,k),f(i-1,j,k));
fi;
end;
Try to evaluate f for small values of i, j and k! -- How far can you get? Can you evaluate f(1,1,1) or f(2,2,2), or can you perhaps write down these values as non-recursive expressions?
The function f is still a computable function -- recall however that there are functions which grow faster than any computable function!
Some values this function takes: f(0,0,0) is 2, f(0,0,1) is 4, f(0,0,2) and f(0,1,0) are both 16, f(0,0,3) is 65536, f(0,0,4) and f(0,1,1) are both 2^65536, f(0,0,5) is 2^2^65536}, and already f(1,1,1) is basically too large to be written down in a non-recursive way. The exercise asks just for some experimentation -- thus there is no solution given.
The 3n+1 conjecture, also known as Collatz conjecture, asserts that iterated application of the Collatz mapping
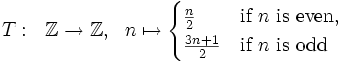
to any given positive integer eventually yields 1. This problem has been posed by Lothar Collatz in the 1930's, and it is still open today.
Investigate Collatz' conjecture by means of computation with GAP, and try to find a proof or a counterexample!
The 3n+1 conjecture is generally believed to be true, but if it is false, this may be for two reasons: firstly, there may be unbounded sequences, and secondly, there may be sequences which run into cycles not containing 1. Jeffrey C. Lagarias has compiled a comprehensive annotated bibliography [Lag07] on this conjecture. The GAP package RCWA [Koh07b] provides a large variety of methods to compute with mappings like the Collatz mapping. We show just how to enter the Collatz mapping and how to compute the sequences we are interested in:
gap> T := RcwaMapping([[1,0,2],[3,1,2]]);
<rcwa mapping of Z with modulus 2>
gap> SetName(T,"T");
gap> Display(T);
Rcwa mapping of Z with modulus 2
n mod 2 | n^T
------------------------------------+------------------------------------
0 | n/2
1 | (3n + 1)/2
gap> Trajectory(T,15,[1]);
[ 15, 23, 35, 53, 80, 40, 20, 10, 5, 8, 4, 2, 1 ]
gap> Trajectory(T,27,[1]);
[ 27, 41, 62, 31, 47, 71, 107, 161, 242, 121, 182, 91, 137, 206, 103,
155, 233, 350, 175, 263, 395, 593, 890, 445, 668, 334, 167, 251, 377,
566, 283, 425, 638, 319, 479, 719, 1079, 1619, 2429, 3644, 1822, 911,
1367, 2051, 3077, 4616, 2308, 1154, 577, 866, 433, 650, 325, 488, 244,
122, 61, 92, 46, 23, 35, 53, 80, 40, 20, 10, 5, 8, 4, 2, 1 ]
There is (of course!) no solution given for this exercise.
generated by GAPDoc2HTML